Долг за какой-то период можно представить геометрически как прямоугольный треугольник, в котором один катет - это основной долг, другой катет - это проценты по основновному долгу, а острый угол, прилежащий к катету, изображающему основной долг, изображает процентную ставку за этот период (его тангенс, умноженный на 100, равен процентной ставке).
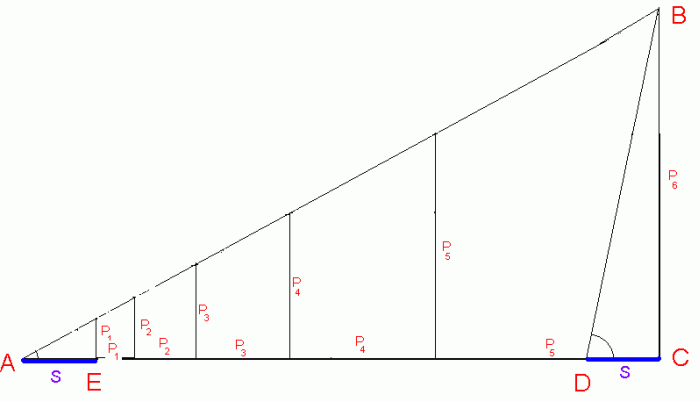
Этот рисунок иллюстрирует рост долга по кредиту, если не отдавать своевременно проценты (без учёта штрафных санкций). Угол A отражает процентную ставку за период (2 месяца), на которые поделен срок кредита (год), угол D - годовую процентную ставку. S - сумма, взятая в долг. Катет BC - проценты по кредиту, если выплатить их единовременно по истечении года. P1, P2, P3 и т. д. - проценты за соответствующее количество периодов.
Сначала надо рассчитать месячную процентную ставку. Пусть S - сумма, взятая в долг, Q - годовая процентная ставка,
Если принять месячную процентную ставку за x, тогда проценты за первый месяц пользования кредитом составят Sx, а долг составит
S+Sx = S(1+x),
или, если обозначить число (1+x) через q,
Sq.
Если не отдать проценты за первый месяц, то они прибавятся к основному долгу, и проценты за второй месяц будут начисляться на всю сумму.
Проценты за второй месяц составят Sqx.
Долг за два месяца составит Sq+Sqx = Sq(1+x) = Sqq = Sq2
Если не отдать проценты и за второй месяц, то они также прибавятся к основному долгу, и проценты за третий месяц будут начисляться на всю сумму.
Проценты за третий месяц составят Sq2x.
Долг за три месяца составит Sq2+Sq2x = Sq2(1+x) = Sq2q = Sq3
Таким образом, долг за 12 месяцев, т. е. за год, составит Sq12
.
В то же время, долг за год составляет S+S(Q:100) = S(1+Q:100).
Т. е. получается следующее:
Sq12 = S(1+Q:100)
q12 = (1+Q:100)
q = (1+Q:100)1/12
Если периодичность погашения составляет не раз в один, а раз в несколько (m) месяцев, то
q = ((1+Q:100)1/12)m
q = (1+Q:100)m/12
В общем случае (например, когда период не кратен месяцу) формула такая:
q = (1+Q:100)z
, где z - число, обратное количеству периодов в году.
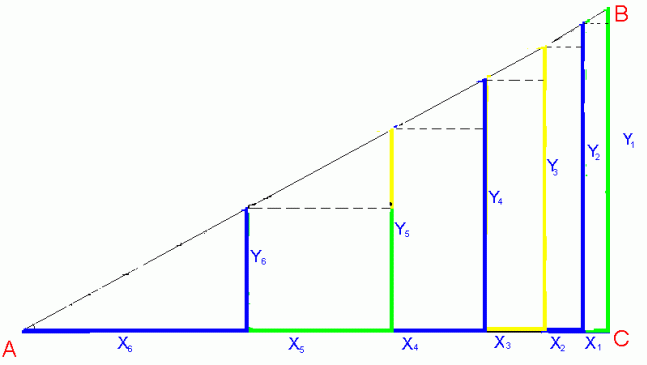
Этот рисунок иллюстрирует схему погашения кредита равными долями за равные промежутки времени. Угол A отражает процентную ставку за период, на которые поделен срок кредита. AC - это сумма кредита (S). Y1 , Y2 , Y3 и т. д. - это проценты, соответственно, за первый, второй, третий и т.д. период. X1 , X2 , X3 и т. д. - это часть основного долга, выплачиваемая вместе с процентами за, соответственно, первый, второй, третий и т.д. период.
Теперь надо рассчитать размер ежемесячного (разового) платежа (V). Чтобы с каждой выплатой долг уменьшался, размер разового платежа должен превышать сумму набежавших за месяц процентов, то есть разовый платёж состоит из двух частей: процентов за пользование деньгами (Y) и части основного долга (X). Т. е. платёж за k-й месяц можно обозначить как Xk+Yk
, а платёж за следующий, т. е.(k+1)-й, месяц - как Xk+1+Yk+1
. А поскольку платежи за все месяцы должны быть одинаковы, то:
Xk+Yk = Xk+1+Yk+1
Xk+1 = Xk+(Yk - Yk+1).
Разницу в процентах между двумя следующими друг за другом месяцами (Yk - Yk+1
) можно вычислить как длину катета в прямоугольном треугольнике, в котором известны тангенс противолежащего угла (q-1) и длина другого катета (Xk), т. е как произведение другого катета на тангенс прилежащего к нему угла:
Yk - Yk+1 = Xk(q-1), т. е.
Xk+1 = Xk+
Xk(q-1) = Xk(1+q-1) = Xkq
Тогда, если выплату из основного долга за первый месяц обозначить X1,
выплата из основного долга за второй месяц составит
X2 = X1q,
выплата из основного долга за третий месяц:
X3 = X2q = X1q2,
...
выплата из основного долга за n-й месяц:
Xn = Xn-1q = X1qn-1,
Таким образом сумму кредита (S) можно записать так
S =
X1 +
X1q +
X1q2 +
... + X1qn-1
S = X1(1+q+q2+...+qn-1)
Отсюда:
X1 = S/(1+q+q2+...+qn-1)
Y1 = V - X1
Y1 = V - S/(1+q+q2+...+qn-1)
А поскольку основной долг за первый месяц - это S, то проценты за первый месяц (Y1
) составят S(q-1); тогда
S(q-1) = V - S/(1+q+q2+...+qn-1)
V = S(q-1) + S/(1+q+q2+...+qn-1)
V = S((q-1) + 1/(1+q+q2+...+qn-1))
(1+q+q2+...+qn-1) - это сумма первых n членов геометрической прогрессии со знаменателем q, поэтому, используя формулу суммы первых n членов геометрической прогрессии
Sn = b1(qn-1)/(q-1),
можно переписать полученную формулу так:
V = S((q-1) + 1/(1(qn-1)/(q-1)))
V = S((q-1) + 1/((qn-1)/(q-1)))
V = S((q-1) + (q-1)/(qn-1))
V = S((q-1)(qn-1) + (q-1))/(qn-1)
V = S(q-1)(qn-1+1)/(qn-1)
V = S(q-1)qn/(qn-1)
Всё, формула получена.